We recently identified the mechanism behind the formation of one particular type of bubbles larger than the rotor-stator gap in a rotor-stator spinning disc reactor. From this experimental and theoretical study we can now accurately model and predict the sizes of these bubbles for a range of viscosities, densities, and process conditions. The model relies on two interesting yet diverse topics in physics… rocket science and the dripping of a tap.
The dripping of a tap
A classical analysis in multiphase flow is the Rayleigh-Plateau instability which describes the growth and break-up of a neck between a droplet and an orifice such as a tap. It was first described by Lord Rayleigh in 1878, but it also describes the dynamics of bubble growth in a rotor-stator spinning disc reactor. The key principle behind the description is the fact that the amplitude of wave-like deformations on the gas-liquid surface can either grow or shrink. The rate at which these amplitudes change is a function of the physical properties of the fluids, and the size of the neck; the longer the distance between the tap and the droplet, the faster these deformations grow, up until the point that the neck pinches off, releasing the large droplet at the end and forming a series of smaller droplets from the original neck.
In a rotor-stator spinning disc reactor, we have the exact mirror image of a dripping tap in a kitchen; in our case, a gas bubble is connected to a gaseous neck in a surrounding liquid. Despite this inverted symmetry, -or perhaps as a result of it-, we found that the same principle from Lord Rayleigh’s leaking tap could be used to describe the moment when a bubble detaches from an orifice in a rotor-stator spinning disc reactor. The photograph on the left clearly shows a growing bubble connected with a neck to the inlet orifice, similar to a droplet that is growing and simultaneously falling from a kitchen tap.
Rocket science
Now we can predict the moment when a bubble detaches from an orifice, we need a model that describes the growth and movement of the bubble in the period until the closure of the neck… and for this we move from the safety of our home kitchen to the realm of the stars and planets; rocket science! Contradictory to a wide-spread belief, rocket science is not that hard and the core of the matter can be summarised in the following simple relationship.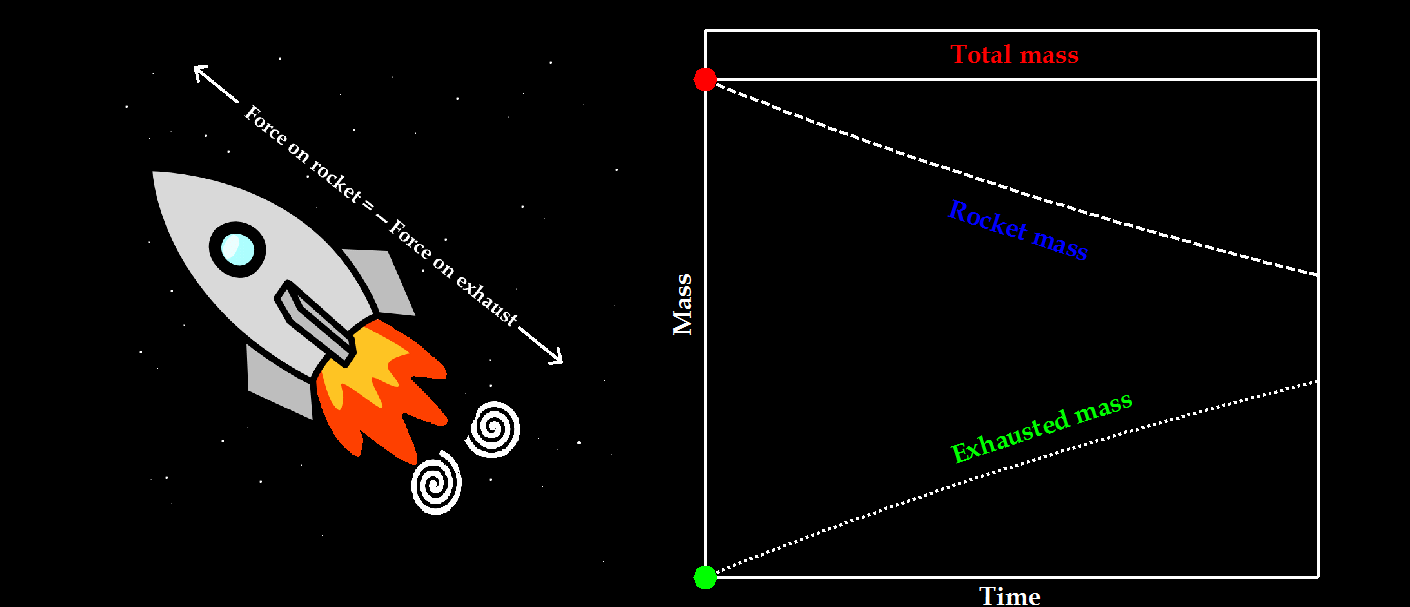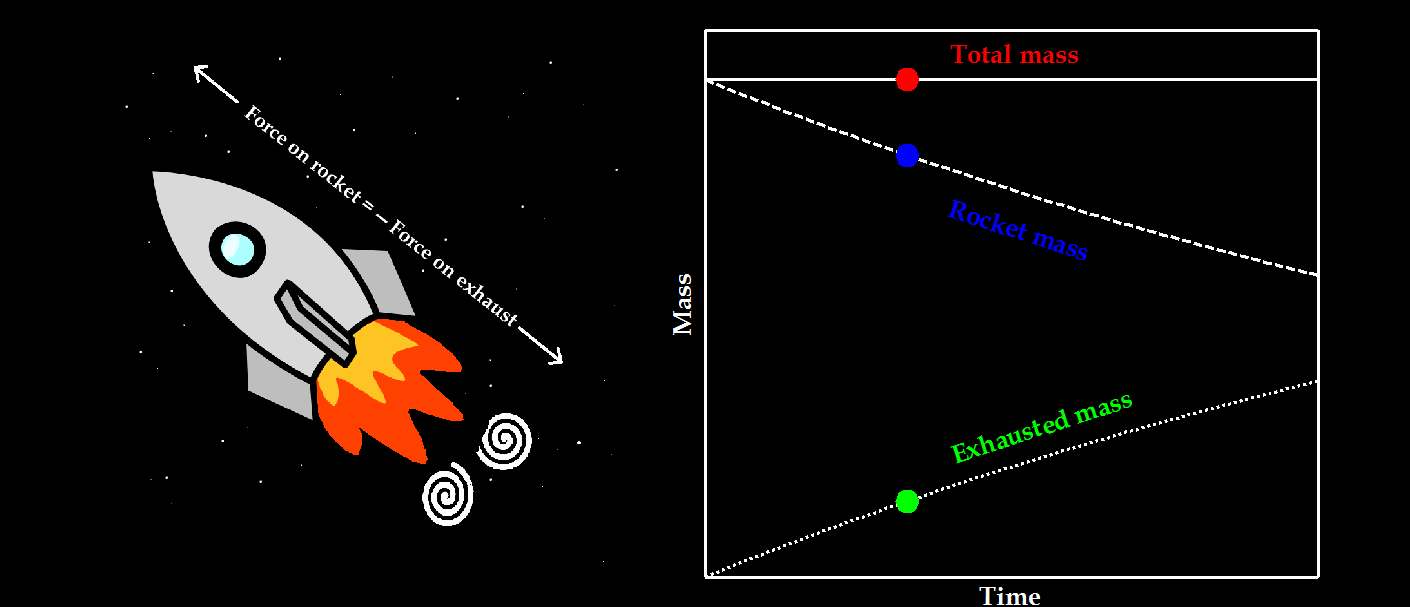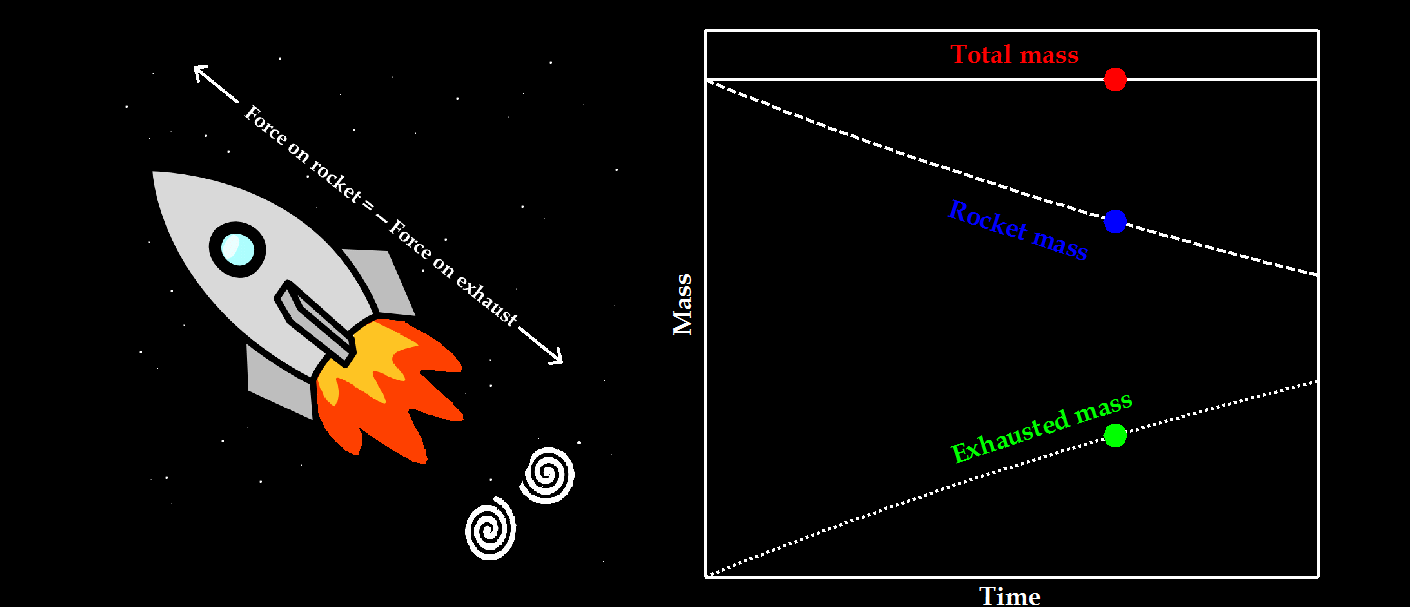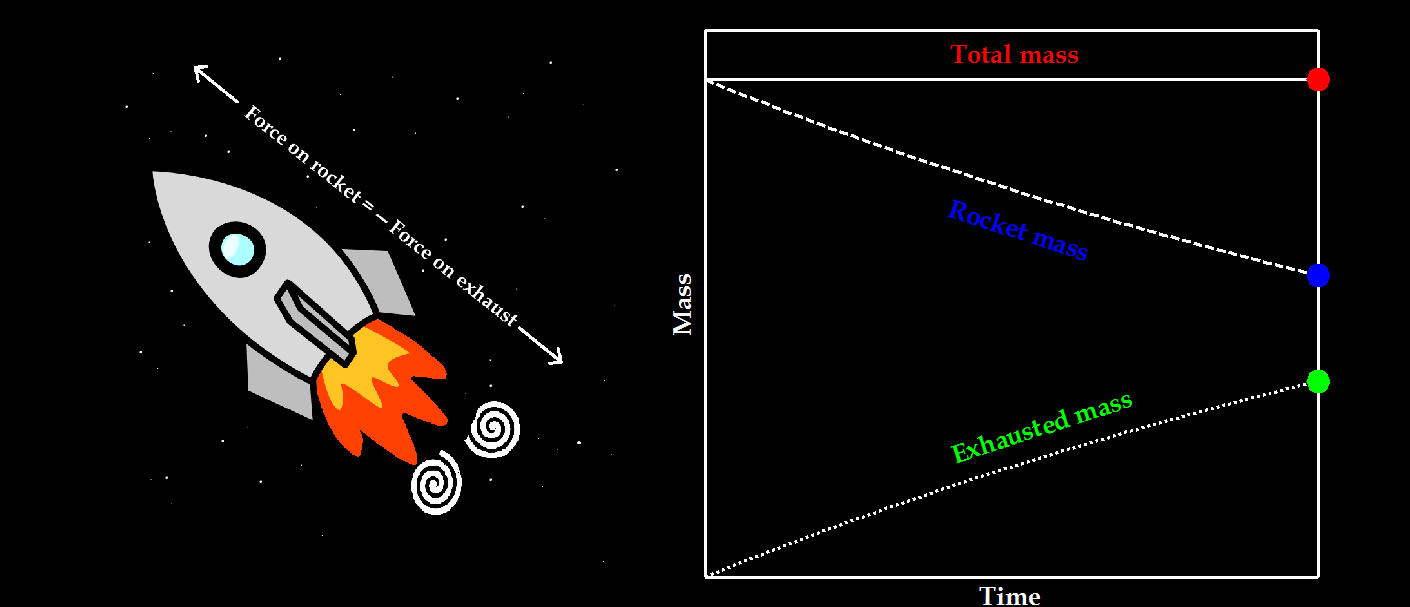
What it comes down to is that Newton’s Second Law only holds for systems with constant mass. In the case of a growing droplet or bubble, or accelerating rocket that is exhausting fuel, the mass that is constant according to Newton’s Second Law is not the mass of the rocket, droplet, or bubble itself, but the total mass. For the rocket this thus includes the exhaust mass, while for the droplet and bubble this includes the feed flow through the neck.
The contents of this blog are based on the following publication:
http://www.sciencedirect.com/science/article/pii/S0009250914000554The GIF for the dripping tap is from: http://www.netanimations.net/