When we slightly modify the Von Kármán similarity transformation to allow time-dependent solutions of the equations of flow between a rotating disc and a stationary wall, it is possible to start with different initial conditions of the flow field and investigate its temporal development. The amount of co- or counter-rotation initially present in the flow field with respect to the motion of the disc determines which final flow field is obtained for steady flow, which were first identified by Holodniok et al. (1977).
Furthermore, when a small random perturbation is added to the steady-flow field it is possible to determine the stability of these flows. By tracking the magnitude of the different source terms for transport of momentum in the Navier-Stokes equations, we can subsequently identify the mechanism (convective or diffusive) and direction (axial, radial, or azimuthal) of transport behind the (de)stabilisation of the flow.
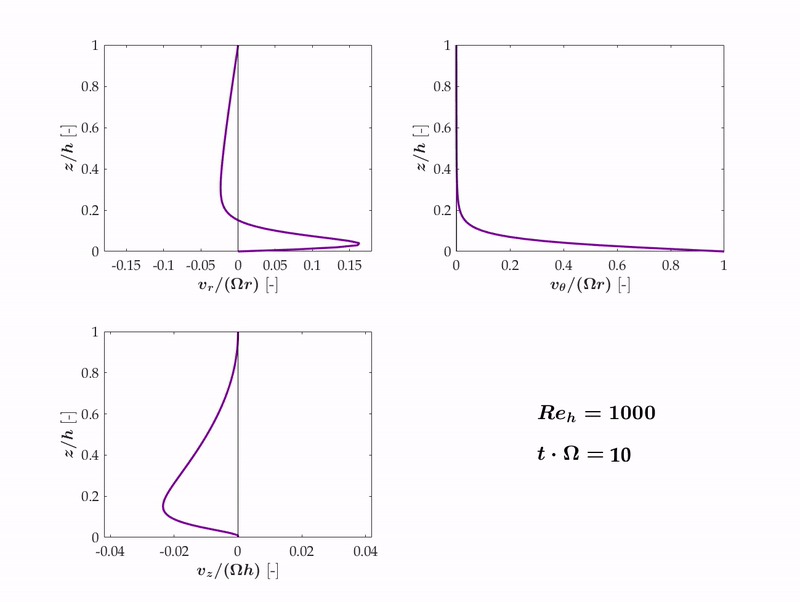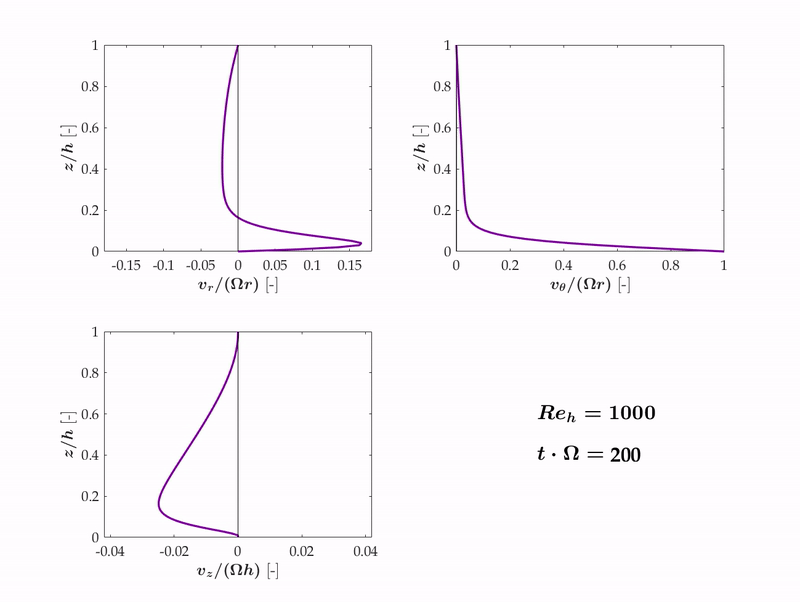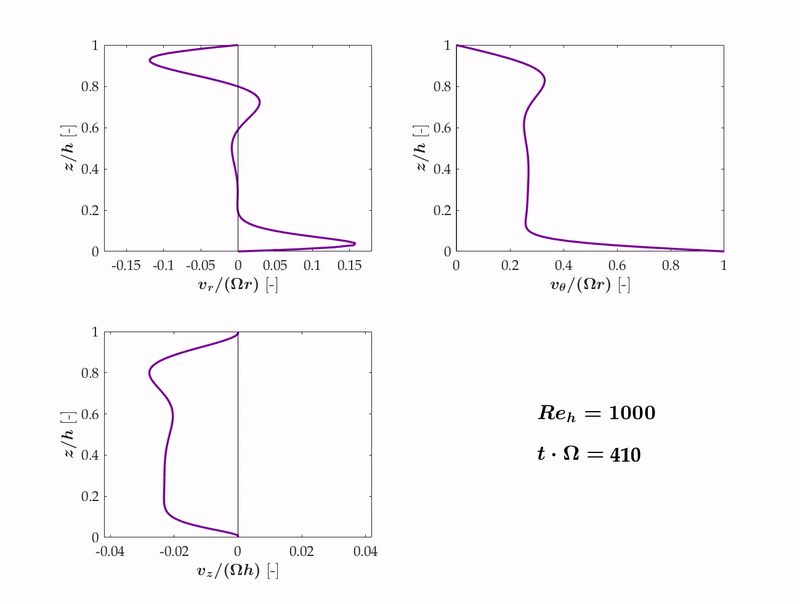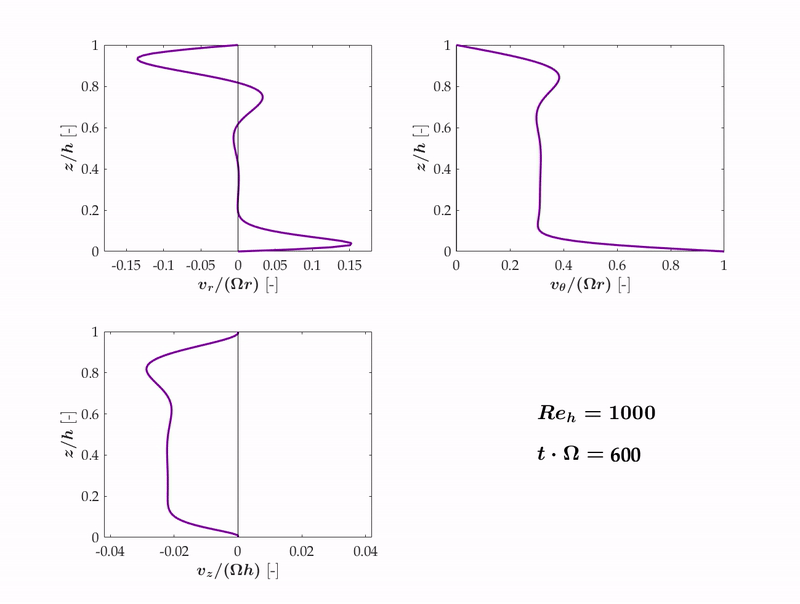
We found that the Stewartson solution for rotor-stator flows is inherently unstable because of the small, but non-zero radially inwards transport of angular momentum by convective means. Via this mechanism, angular momentum is transported radially inwards and by conservation, the azimuthal velocity increases, triggering an instability that leads from Stewartson flow to Batchelor flow.
The following animation for Reh = 103, shows the three components of velocity versus time during the transition of Stewartson to Batchelor flow.
The contents of this blog are based on the following publication:
http://aip.scitation.org/doi/abs/10.1063/1.4812704
